(a+b+c)^3 formula 105638-Algebra formula (a+b+c)^3 pdf
Explanation Use the Binomial expansion (note the exponents sum to the power in each term) (xy)^3 = _3C_0x^3y^0 _3C_1x^2y^1 _3C_2x^1y^2 _3C_3x^0y^3 Remember 3!Explanation Use the Binomial expansion (note the exponents sum to the power in each term) (xy)^3 = _3C_0x^3y^0 _3C_1x^2y^1 _3C_2x^1y^2 _3C_3x^0y^3 Remember 3!Q = (x 2;y 2) you can obtain the following information 1The distance between them, d(P;Q) = p (x 2 x

Ppt Quadratic Equations Powerpoint Presentation Free Download Id
Algebra formula (a+b+c)^3 pdf
Algebra formula (a+b+c)^3 pdf-= 2*1 = 2, 1!Calculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex roots
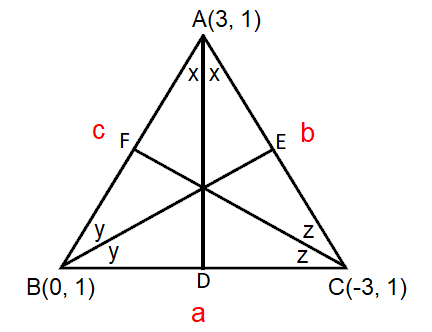


Incenter Of A Triangle
B C 1 Data Formula Description (Result) 2 =/A3 Divides by 12 (1250) 3 12Here a = 3x, b = 2y and c = z 3x (2y) (z) 2 = (3x) 2 (2y) 2 (z) 2 2 (3x) (2y) 2 (2y) (z) 2 (z) (3x) = 9x 2 4y 2 z 2 – 12xy 4yz – 6zx 2 Simplify a b c = 25 and ab bc ca = 59 Find the value of a 2 b 2 c 2 Solution According to the question, a b c = 25N = y x!
N = yn xn x0 = 1;(a) the anesthetic halothane, C 2 HBrClF 3 (b) the herbicide paraquat, C 12 H 14 N 2 Cl 2 (c) caffeine, C 8 H 10 N 4 O 2 (d) urea, CO(NH 2) 2 (e) a typical soap, C 17 H 35 CO 2 Na Determine the number of moles of compound and the number of moles of each type of atom in each of the following (a) 250 g of propylene, C 3 H 6 (b) 306 × 10 −3(0!)) = (3!)/ ( (3)!1) = 1
(0!)) = (3!)/ ( (3)!1) = 1Ma=1 mb=25 mc=2 triangle calc by three medians ha=2, hb=165 hc=132 triangle calc by three heights a=7 β=40 mc=5 triangle calc by one side, one angle, and one median abc=234 T=25 a triangle where the known side ratio, and its areaIn algebra, a quadratic equation is any polynomial equation of the second degree with the following form ax 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers



Perimeter Of A Triangle Definition Formula And Examples
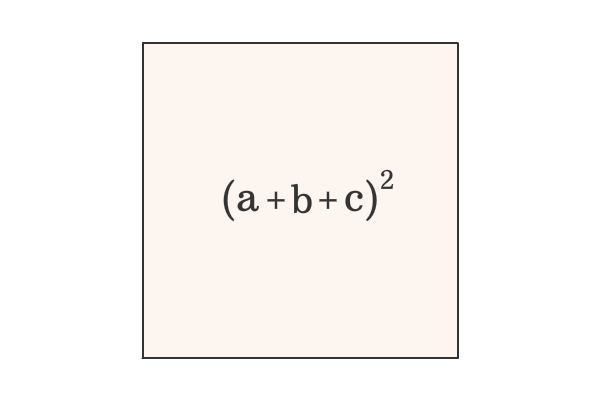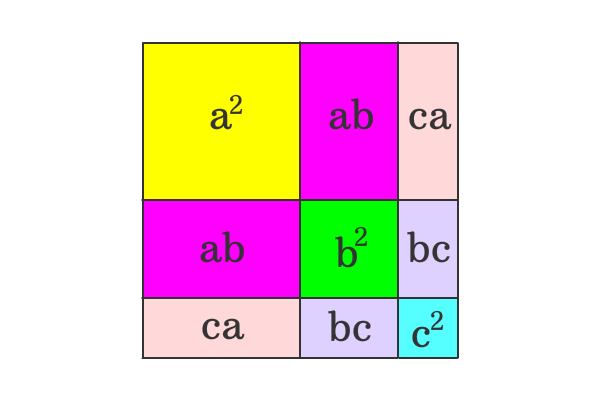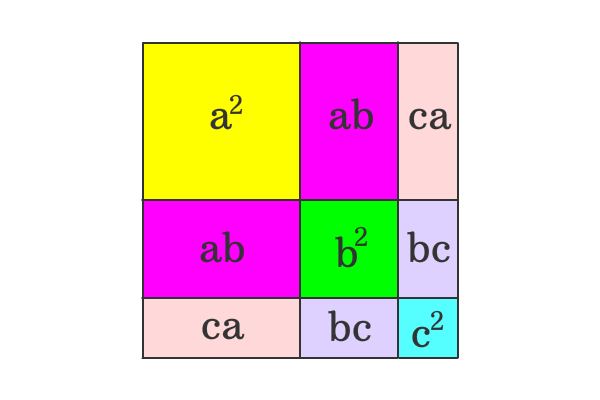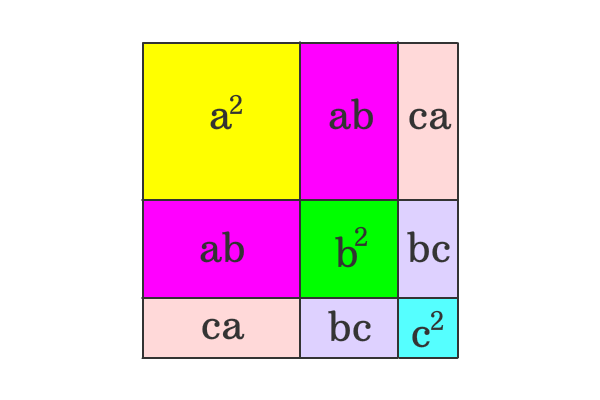


Proof Of A B C Formula In Geometric Method
X6= 0 x y!${\left( {a b c} \right)^2} = {a^2} {b^2} {c^2} 2ab 2ac 2bc$ ${\left( {a b} \right)^3} = {a^3} 3{a^2}b 3a{b^2} {b^3};{\left( {a b} \right)^3} = {a^3} {b^3} 3ab\left( {a b} \right)$ ${\left( {a b} \right)^3} = {a^3} 3{a^2}b 3a{b^2} {b^3}$ ${a^3} {b^3} = \left( {a b} \right)\left( {{a^2} ab {b^2}} \right)$Calculate squares 1 1 = c2 11=2 2 = c2 Swap sides c2 = 2 Square root of both sides c = √2 Which is about c = It works the other way around, too when the three sides of a triangle make a2 b2 = c2, then the triangle is right angled



21 A Compound Contains Three Elements A B And C If The Oxidation Of A 2 B 5 And C 2 The Possible Formula Of The Compound Is 1 43 B4c 2 2 A3 4 2 3 A 3 2 4 Abc



3 C B
A = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) {\displaystyle A= {\frac {4} {3}} {\sqrt {\sigma (\sigma m_ {a}) (\sigma m_ {b}) (\sigma m_ {c})}}} Next, denoting the altitudes from sides a, b, and c respectively as ha, hb, and hc, and denoting the semisum of the reciprocals of the altitudes as H = 1 / 2 (h−1= 1 _3C_0 = (3!)/ ( (30)!Q = (x 2;y 2) you can obtain the following information 1The distance between them, d(P;Q) = p (x 2 x
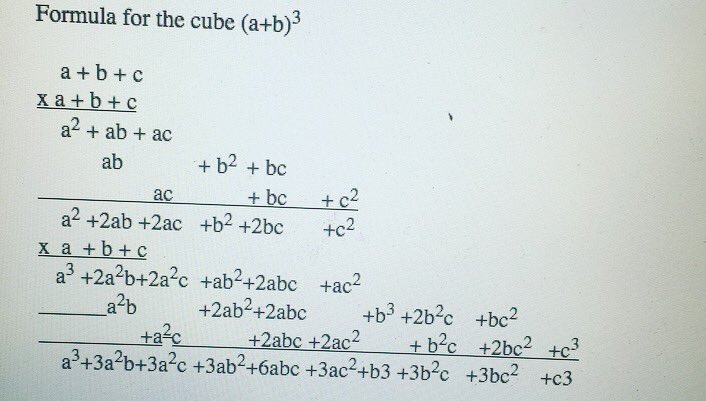


Eve Mendolia The Trinomial Cube Is A B C 3 Montessori Apsisawesome Apsdrew Apsvirginia Apsmath Suptpkm



Formula Of A B C Whole Cube Math Polynomials Meritnation Com
Video Lesson Khan Academy Video Quadratic Formula 1;N = y x!5(a b c)2 = a2 b2 c2 2ab2bc 2ca 6(a b c)3 = a3 b3 c33a2b3a2c 3b2c 3b2a 3c2a 3c2a6abc 7a2 b2 = (a b)(a – b ) 8a3 – b3 = (a – b) (a 2 ab b2 ) 9a3 b3 = (a b) (a 2 ab b2 ) 10(a b)2 (a b) 2 = 4ab 11(a b)2 (a b) 2 = 2(a 2 b2 ) 12If a b c =0, then a3 b3 c3 = 3 abc INDICES AND SURDS 1 am a n = a m n 2


Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3



2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download
= 2*1 = 2, 1!= ab c a b c!= ac b a c c d = ad Properties of Absolute Valuebc bd a b c = a c b c a b!N = yn xn x0 = 1;
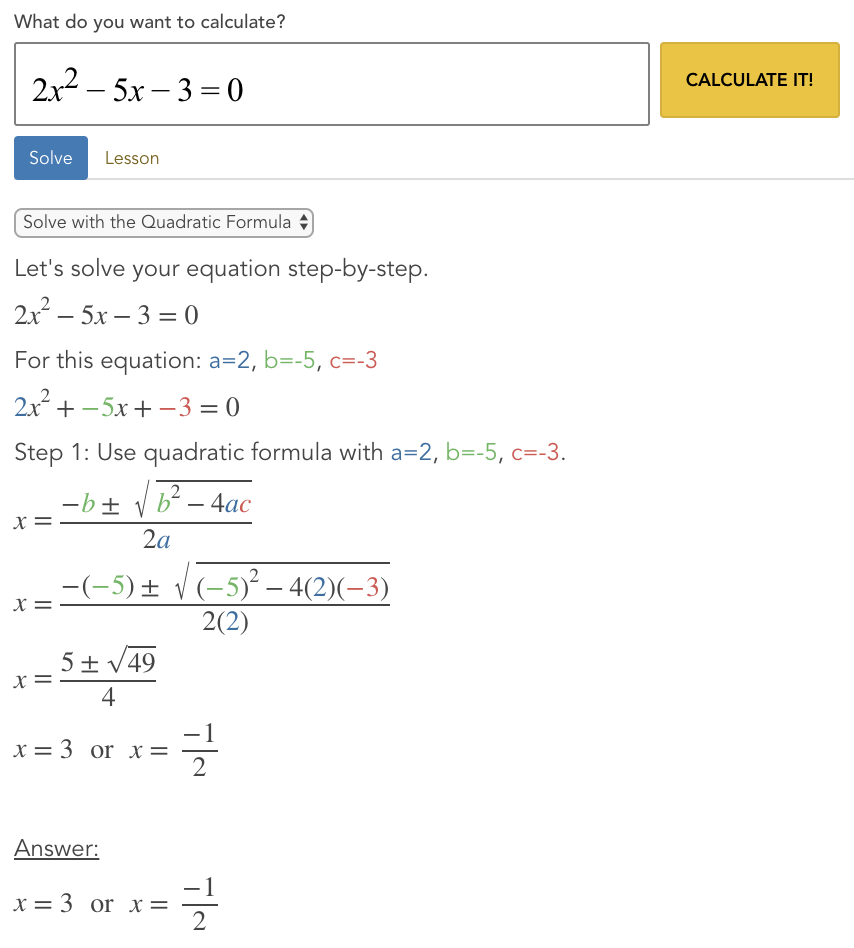


Quadratic Formula The Mathpapa Guide
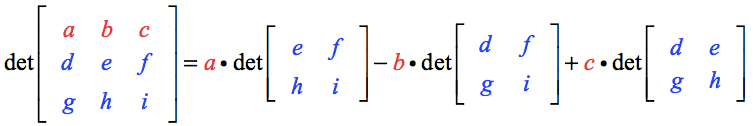


Determinant Of 3x3 Matrix Chilimath
X6= 0 x y!In this case, a = 2, b = –4, and c = –3 Then the answer is x = –058, x = 258 , rounded to two decimal places Warning The "solution" or "roots" or "zeroes" of a quadratic are usually required to be in the "exact" form of the answerC = a bc a b c d = ad bc bd a b c d = b a d c ab ac a = b c;


A B C 3 Class 9 Formula Youtube



Incenter Of A Triangle
C = a bc a b c d = ad bc bd a b c d = b a d c ab ac a = b c;Both primitive Pythagorean triples and nonprimitive Pythagorean triples can be generated by the Pythagorean triples formula Pythagorean triples formula is given as (a, b, c) = (m 2 − n 2 );(m 2 n 2 ) Where, m and n are two positive integers and m > n



Factorise A 3 B C 3 B 3 C A 3 C 3 A B 3



If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum
A6= 0 a b c!(a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 (a b – c) 2 = a 2 b 2 c 2 2ab – 2bc – 2ca (a – b c) 2 = a 2 b 2 c 2 – 2ab – 2bc 2caThe triangle perimeter is the sum of the lengths of its three sides p = a b c = 3 5 7 = 15 p = abc = 357 = 15 p= abc = 35 7 = 15 3 Semiperimeter of the triangle The semiperimeter of the triangle is half its perimeter



1 If A B C 6 Then Find 2 A 3 2 B 3 2 C 3 3 2 A 2 B 2 C 2multiple Choice If 2 A 2 B 2 A B 2 Then A A B 0 B A B C 2a B D Ab 0 Mathematics Topperlearning Com Ewq7ff



Solved Question 2 A Given That In The Triangle Abc Ang Chegg Com
Determine the values of a, b, and c for the quadratic equation 4x 2 – 8x = 3 answer choices a = 4, b = 8, c = 3 a = 4, b =8, c =3 a = 4, b = 8, c = 3 a = 4, b = 8, c = 3 s Question 2A 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc Some not so Common FormulasN = xn yn 1 x n = xn xn xm = xn m x n = 1 xn Properties of Radicals n p x= x1n n p xy= n p xn p y m q n p
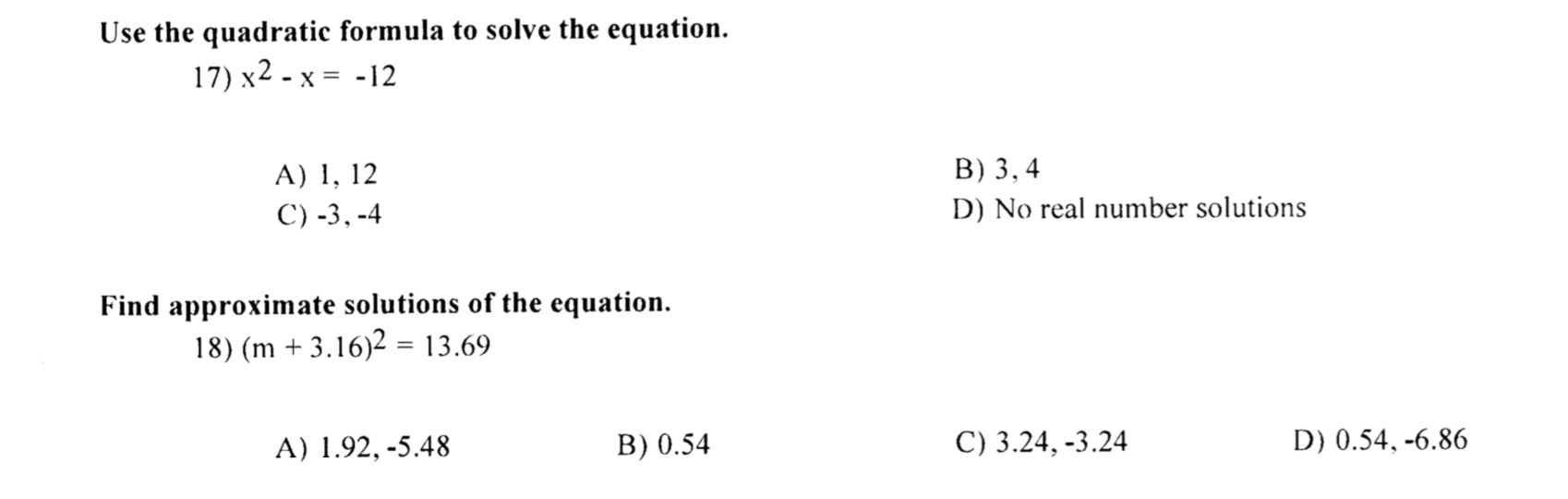


Solved Use The Quadratic Formula To Solve The Equation 1 Chegg Com


Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau
3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);= 1 and 0!A 3 b 3 c 3 – 3abc = (a b c)(a 2 b 2 c 2 – ab – bc – ca) If a b c = 0, then the above identity reduces to a 3 b 3 c 3 = 3abc Few Other Mathematical Formula


The Pythagorean Theorem



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
(a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b) 3 = a 3 3a 2 b 3ab 2 b 3;(question mark) means any item It is like a "wildcard"3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);



Formulas For Generating Pythagorean Triples Wikipedia



Toppershala Algebra Formulas Facebook
X³ (abc) x² (abbcca) xabc a² b² c² a b b c c a = ½ (ab)²(bc)²(ca)² (abc) (a² b² c² a bb cc a) = a³ b³ c³ 3 a b c Logarithms Math Formulas Product rule log ₐ (m n) = log ₐ m log ₐ nCalculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex rootsQ Determine the values of a, b, and c for the quadratic equation 4x 2 – 8x = 3 *remember right side should =0 answer choices a = 4, b = 8, c = 3 a = 4, b =8, c =3 a = 4, b = 8, c = 3



What Is The Formula Of A B C Cube Math Algebraic Expressions And Identities Meritnation Com



Math 3510 Textbook Notes Spring 19 Chapter 4 Transpose Formula 4 Coefficient Matrix
The Cubic Formula The Cubic Formula The quadratic formula tells us the roots of a quadratic polynomial, a poly nomial of the form ax2 bx c The roots (if b24ac 0) areb p b24ac 2a andb p b24ac 2a The cubic formula tells us the roots of a cubic polynomial, a polynomial of the form ax3bx2cxd It was the invention (or discovery, depending on your point of view) of the complex numbers in the 16th century that allowed mathematicians to derive the cubic formula, and it was for thisThe Pythagorean triples formula has three positive integers that abide by the rule of Pythagoras theorem It is most common to represent the Pythagorean triples as three alphabets (a, b, c) which represents the three sides of a triangle The right triangles constructed with the sides 'a', 'b' and 'c' are called Pythagorean triangles= 3*2*1 = 6, 2!



Answered Let Bo B Bz Be The Sequence Bartleby


Www Stmarysguwahati Org In Notes1 9 Ad Maths Pdf
A = 2, b = 3, c = −1 Now that the equation is in standard form, you can read the values of a, b, and c from the coefficients and constant Note that since the constant 1 is subtracted, c must be negative Answer 2x 2 3x – 1 = 0;A3 b3 c3 = (a b c) (a2 b2 c2 – ab – bc – ca) 3abc My Mug (of) formulas Just another WordPresscom weblog « Inradius of a triangleA³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³ then a³ b³ = (a b)³ – 3ab(a b) = (a b)(a b)² – 3ab = (a b)(a² 2ab b² – 3ab) = (a b)(a² – ab b² )


Search Q Formula Abc C2 Tbm Isch


Ssc Quantitative Aptitude Tricks Algebraic Equations
C d!= ad bc Properties of Exponents x nx m= x (xn)m = xnm (xy) n= xyn xn m = x1 m n = xn 1 m x y!C d!= ad bc Properties of Exponents x nx m= x (xn)m = xnm (xy) n= xyn xn m = x1 m n = xn 1 m x y!= ab c a b c!= ac b a c c d = ad Properties of Absolute Valuebc bd a b c = a c b c a b!



A B C 3 Formula Proof



A Compound Contains Three Elements X Y And Z The Oxidation Number Of X Y And Z Are 3 5 And 2 Respectively The Possible Formula Of The Compound Is
= 1 and 0!If column B = Ross and column C = 8 then in cell AB of that row I want it to show 13, If column B = Block and column C = 9 then in cell AB of that row I want it to show 12 Answer You can create your Excel formula using nested IF functions with the AND functionSolve an equation of the form a x 2 b x c = 0 by using the quadratic formula x = − b ± √ b 2 − 4 a c 2 a StepByStep Guide Learn all about the quadratic formula with this stepbystep guide Quadratic Formula, The MathPapa Guide;



Question Prove That A B C 3 A3 C3 3 A B B C C A Mathematics Topperlearning Com We5wwhmm



Algebra Formula Definition Formulas And Examples
Recall the formula ` (abc)^2 = a^2 b^2 c^2 2 (ab bc ca)` Given that `a^2 b^2 c^2 = 250 , ab bc ca = 3 ` Then we have ` (abc)^2 = a^2 b^2 c^2 2 (ab bcca)` ` (abc)^2 = 250 2 (3)` ` (abc)^2 = 256` ` (abc) =± 16`Simplify the all Multiplication one by one \((abc)^3 = a \times (a^2b^2c^2 2ab 2bc 2ca)\\ b \times (a^2b^2c^2 2ab 2bc 2ca)\\ c \times (a^2b^2c^2 2ab 2bc 2ca) \) \(=> (abc)^3 = (a^3ab^2ac^2 2a^2b 2abc 2ca^2)\\ b \times (a^2b^2c^2 2ab 2bc 2ca)\\ c \times (a^2b^2c^2 2ab 2bc 2ca) \)Solution By Pascal's formula, n 2 C r = n 1 C r 1 n 1 C r Applying Pascal's formula again to each term on the right hand side (RHS) of this equation, n 2 C r = n C r 2 n C r 1 n C r 1 n C r, for all nonnegative integers n and r such that 2 £ r £ n 2 Use this formula and Pascal's Triangle to verify that 5 C 3 = 10 5 C 3 = 3 C 1 2(3 C 2) 3 C 3



Prove That A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2



64 Useful Math Stations Teaching Info In Studying Math Basic Math Math Methods
A = 2, b = 3, c = −1In algebra, a quadratic equation is any equation that can be rearranged in standard form as a x 2 b x c = 0 {\displaystyle ax^{2}bxc=0} where x represents an unknown, and a, b, and c represent known numbers, where a ≠ 0 If a = 0, then the equation is linear, not quadratic, as there is no a x 2 {\displaystyle ax^{2}} term The numbers a, b, and c are the coefficients of the equation and may be distinguished by calling them, respectively, the quadratic coefficient, the linearA 4 – b 4 = (a – b)(a b)(a 2 b 2)



Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A Youtube


Show That The Points A B C B C A C A B Are Collinear Coordinate Geometry Maths Class 10
= 3*2*1 = 6, 2!Algebraic Formula Sheet Arithmetic Operations ac bc= c(a b) a b!(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2) a 3 b 3 = (a b)(a 2 – ab b 2) (a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 (a – b) 4 = a 4 – 4a 3 b 6a 2 b 2 – 4ab 3 b 4;



Identities Math Methods Learning Mathematics Math Formula Chart


Section Formula A Plus Topper
$$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) abc$$ It doesn't look like I made careless mistakes, so I'm wondering if the statement asked is correct at all algebraprecalculusOnly {a,b,c} is missing because that is the only one that has 3 from the list a,b,c The "pattern" Rule The word "pattern" followed by a space and a list of items separated by commas You can include these "special" items?A = 2 b = 3 c = 4 Therefore, s = 2 3 4 2 = 9 2 = 45 So, area = √45⋅ (45− 2)⋅ (45 −3) ⋅(45 −4) = √475 = 29u2



A B C 3 Expansion



Multinomial Expansion
A 1,1 ×b 1,1 a 1,2 ×b 2,1 a 1,3 ×b 3,1 = c 1,1 The dot product is performed for each row of A and each column of B until all combinations of the two are complete in order to find the value of the corresponding elements in matrix C For example, when you perform the dot product of row 1 of A and column 1 of B, the result will be c 1,1 of matrix CN = xn yn 1 x n = xn xn xm = xn m x n = 1 xn Properties of Radicals n p x= x1n n p xy= n p xn p y m q n pAlgebraic Formula Sheet Arithmetic Operations ac bc= c(a b) a b!



Prove That Tex A B C 3 A 3 B 3 C 3 3 A B B C C A Tex Brainly In



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Algebra Formulas Algebra Notes Algebra Help
A6= 0 a b c!There are four elements, a, b, c, d so we can choose 3 of them from 4, in 4 ways There are therefore four of these The sum of the coefficients is 4·6=24 We add up the coefficients to check that they sum to (1111) 3 =64 We can also check the part sums, as aboveSolution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3 (2a) (3b) (5c) And this represents identity a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c


Using Distance Formula Prove That The Following Points Are Collinear I A 4 3 1 B 5 7 6 And C 3 1 8 Sarthaks Econnect Largest Online Education Community



Solved Solve The Formula For The Specified Variable 13 Chegg Com
C (n,r) » a^3 b^3 c^3 a 3 b 3 c 3 = (a b c) (a 2 b 2 c 2 – ab – bc – ca) 3abc s Algebra, cube, sum, sum of cubesA³ a²b a²c 2a²b 2ab² 2abc 2a²c 2abc 2ac² ab² b³ b²c 2abc 2b²c 2bc² ac² bc² c³ This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of eachMATHEMATICAL FORMULAE Algebra MATHEMATICAL FORMULAE Algebra 1 (ab)2=a22abb2;a2b2=(ab)2−2ab 2 (a−b)2=a2−2abb;a2b2=(a−b)22ab 3 (abc)2=a2b2c22(abbcca) 4 (ab)3=a3b33ab(ab);a3b3=(ab)−3ab(ab) 5



If A B C 0 Then A B C 3 27abc How Mathematics Topperlearning Com 3wlz7ftt



How To Prove The Identiy A3 C3 3abc Math Polynomials Meritnation Com
= 1 _3C_0 = (3!)/ ( (30)!Formula A∪B = {a1,a2,a3,a4,,an} with ai∈A or ai∈B,i=1,2,3,n Where, A and B represents the set A and set B Related CalculatorFrom Lagrange's formula it follows that the vector triple product satisfies a × ( b × c ) b × ( c × a ) c × ( a × b ) = 0 {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0} }


A Triangle Has Sides Of Lengths 3 Cm 4 Cm And 5 Cm What Is The Area Of The Circle Inscribed In The Triangle M Cube Mathematics By Maheshwari



Ppt Quadratic Equations Powerpoint Presentation Free Download Id
Quadratic Formula For an equation of the form \(ax^2bxc=0\), you can solve for x using the Quadratic Formula $$ x = \frac{b \pm \sqrt{b^24ac}}{2a} $$ Binomial Theorem \((ab)^1= a b\) \((ab)^2=a^22abb^2\) \((ab)^3=a^33a^2b3ab^2b^3\) \((ab)^4=a^44a^3b6a^2b^24ab^3b^4\) Difference of Squares \(a^2b^2=(ab)(ab)\) Rules of Zero


New Page 1



All Formula With Example Of Algebric Expression Of Cube Brainly In



Conventional Unit Cell Of E Carbide With A Fe 6 C 2 B Fe 12 C 5 Download Scientific Diagram



Mathematical Formula For Competitive Exams Math Shortcut Tricks



I Found K A B B C C A But What Is The Co Fa Chegg Com



A 3 3 B 2 C 2 25 B 3 3 A 2 C 2 25 C 3 3 A 2 B 2 25 Find A B C Where A B C Are All Real Numbers Plz Solve This Hurry Sir Mathematics Topperlearning Com 4ko43xnn



Vector Triple Product Definition Formula Proof Solved Problems



Basic Formulae Square Formula 2 Variables


Math Scene Equations Iii Lesson 2 Quadratic Equations
.png)


All Mathematical Formula Chart The Future
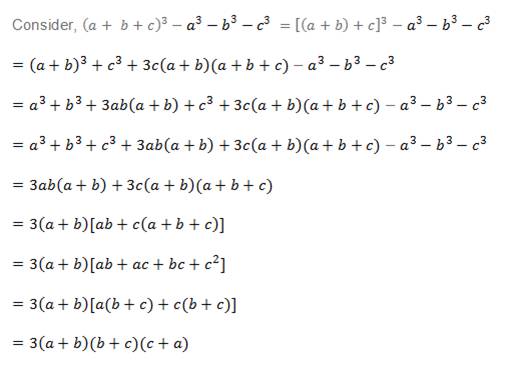


Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9


What Is The Formula For Math A B C 3 Math Quora



If The Roots Of The Equation A 2 X 2 2 B 2 Ca X C 2 Ab 0
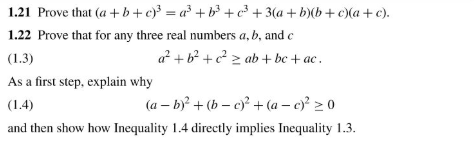


Solved 1 21 Prove That A B C 3 A3 C3 3 A B Chegg Com


What Is The Perfect Formula For A B C Cube Quora



Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube


Quadratic Formula Teacher Guide



What Is The Expansion Of A B C 3 Quora


What Is The Formula Of Math A 3 B 3 Math Quora


Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau



Formula Of A3 C3 Brainly In



Cubic Equation Wikipedia



Answered Ax B 3 Suppose F X Cx D A Find Bartleby



Prove A B C 3 A 3 B 3 C 3 3 A B B C C A Mathematics Topperlearning Com 9j3ovqff


What Is The Formula Of Math A 3 B 3 Math Quora



A3



If A B C 0 Then A 3 B 3 C 3 0 How Quora


If A B C 0 But Abc Don T Equal 0 Then A 2 B 2 Ca C 2 Ab Brainly Com



A 3 B 3 C 3 Formula Brainly In



Algebra Problems Part 3 Questions Based On A B C 3abc A B C A B C Ab Ca Formula Youtube


With The Help Of The Flow Chart Given Below Solve The Equation X 2 2 3 X 3 0 Using The Formula Sarthaks Econnect Largest Online Education Community



Formula Centroid Of A Generalized Fuzzy Triangular Mathematics Stack Exchange


Q Tbn And9gcsn3hmt8qz Utmzoqeyjo2k4rnk95kuib8fxbhmd Uvs2llqap Usqp Cau
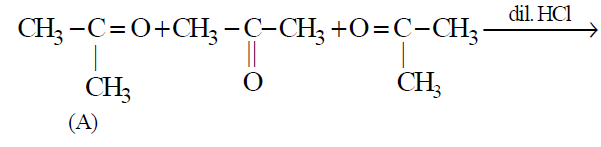


An Organic Compound A Has The Molecular Formula C3h6o It



In The Study Of Chlorination Of Propane Four Product A B C D



If A 2 B 2 C 2 Ab Ca 0 A B C In R Then Find The Value O



Sat Ii Math Level 2 Test 02 Solution 1 The Positive Zero Of Y X 2 2x 3 5 Is To The Nearest Tenth Equal To A 0 8 B I C 0 7 D Ppt Download



3 1 Functions A Relation Is A Set Of Ordered Pairs X Y Example The



Yp Tutorials Important Formulas In Algebra Are You Aware Facebook



What Are Various Forms To Write A B C A Whole Cube Quora


Server Math Umanitoba Ca Claya 2132 Week10 Pdf



Suppose We Define The Definite Integral Using The Following Formul
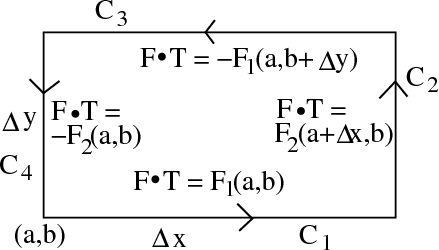


Calculating The Formula For Circulation Per Unit Area Math Insight



Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube



Optimized Structures Of Pristine C 3 N Along With Their Spin Density Of Download Scientific Diagram


A B C 3 Formula Expansion



Mathematics Introduction And Formulas



Quadratic And Cubic Sequences Solutions Examples Videos Worksheets Games Activities


Wl Apsva Us Wp Content Uploads Sites 38 17 08 Chap Lin Quad Fncs Notes 18 Pdf



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



How A 3 B 3 C 3 3abc Mathematics Topperlearning Com



Ex 12 3 4 Using Section Formula Show That Points A 2 3 4 B



A 3 B 3 C 3 3abc Formula A B 2 A 2 B 2 2ab Proof Derivation Of Algebraic Identities Youtube Youtube



Important Mathematical Formulas


A B C 3 Ka Formula


Evaluate The Formula Vectors A X A X C A C B A B C If Sarthaks Econnect Largest Online Education Community



コメント
コメントを投稿