上 公差 二乗平均 194831-公差 二乗平均 3σ
最小二乗法の代数学的性質(図示) (x,y) ① 回帰直線は 標本平均点を通る ③④残差は = 回帰直線のまわりに 偏りなく分布 ②残差の 総和ゼロ (参考) 残差が と負に相関 x y y x が大きいほど負の残差が 出やすくなっている ↑ 最小二乗法ではこうならない ( ,ˆ)二乗和平方根(Root Sum Squire) 起こり得る可能性の少ない公差の最大・最小領域の寸法を含めずに、それぞれの公差を二乗して積み上げ、平方根公差の 2448 ㎡から逆算すると,この場合の辺長は 1391 m から 1409 m の間である必要があります。面積で公差範囲内であるためには,位置誤差,辺長誤差がすべて平均二乗誤差の範囲にあってもその公差範囲に入ることは難しいようです。 現実的な問題

誤差と相対誤差 ライブラリ Opeo 折川技術士事務所
公差 二乗平均 3σ
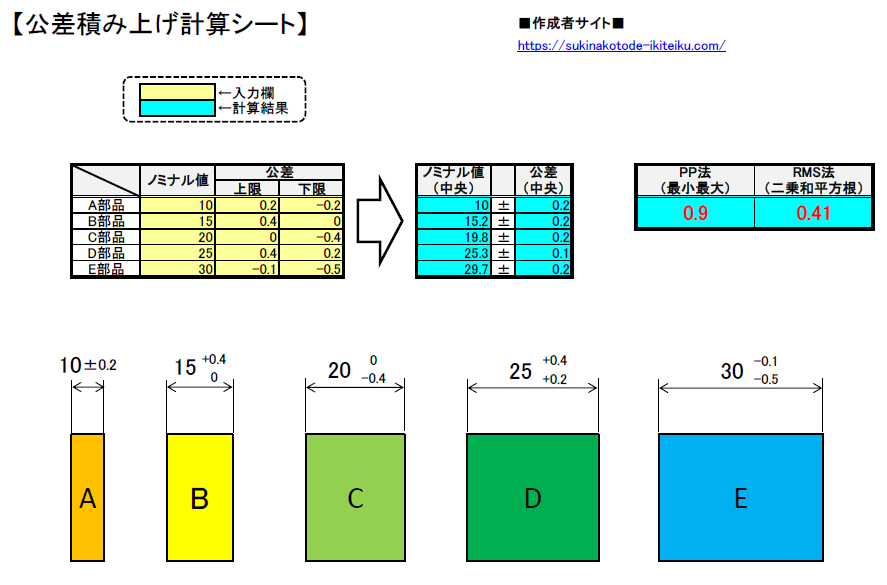
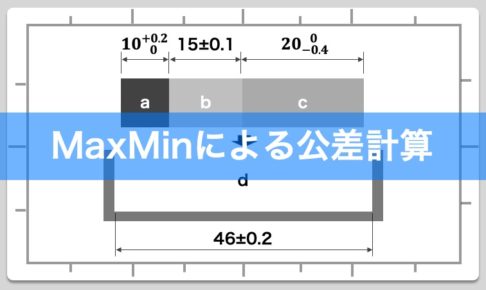
公差 二乗平均 3σ-公差計算 二乗平均 製品設計のいろは2乗和平方根で公差計算を行うための3つの 公差計算を行う際、MaxMinによるワースト値を用いた計算方法と、統計学における正規分布の考え方を用いた計算方公差の積み上げ計算方法については、大きく2種類あります。 1つ目は 「PP法」 というもので、peak to peak (ピークトゥーピーク)の略で、公差内での最小状態と最大状態を計算する方法になります。 こちらは単純に足し算していくだけなので、簡単に計算する事が出来ます。 2つ目は 「RMS法」 というもので、root mean squareの略で、二乗平均平方根や二乗和平方根と呼ばれ



公差分析編 ライブラリ Opeo 折川技術士事務所
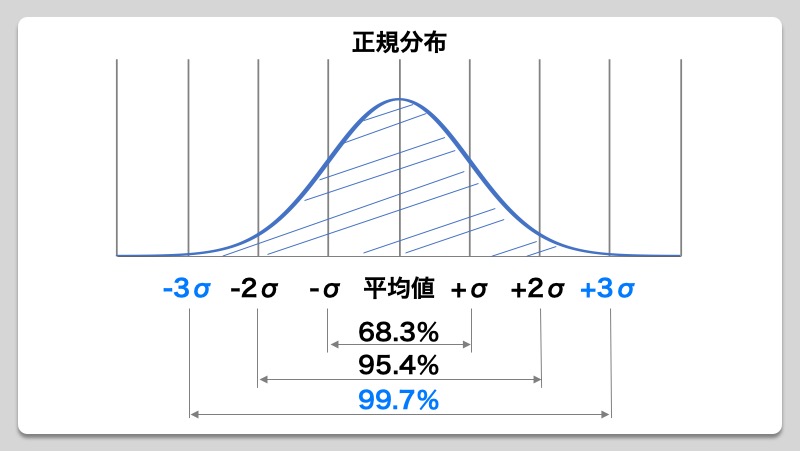
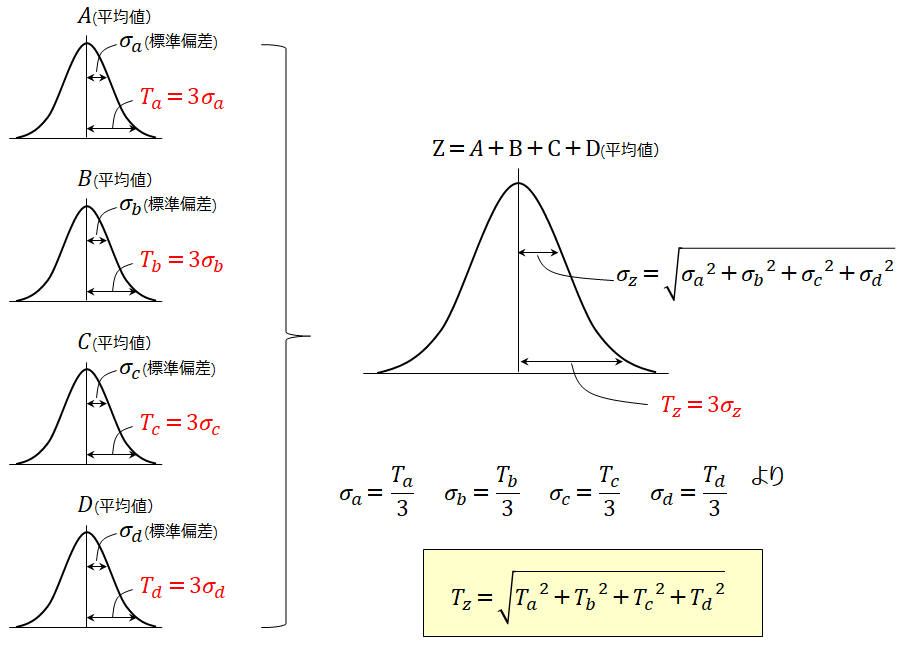
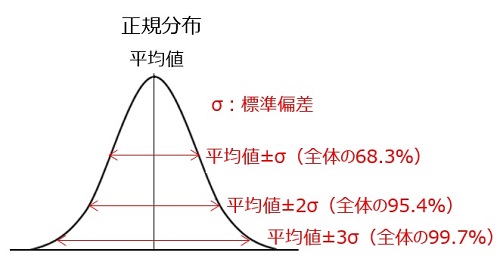
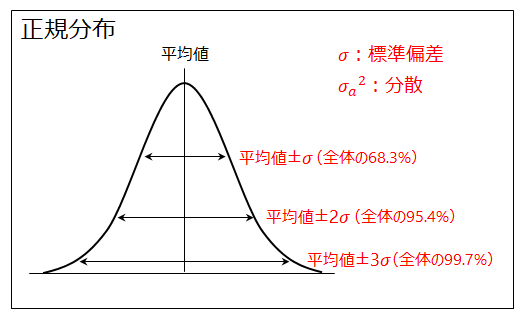
累積公差は、基本は最大最小値で計算するが、 遊びが問題になる場合 k×srss(wi) で計算する。 k をどの程度にするかは、公差 wi に対し実際の分布をどう管理するかという問題なので、 本来なら製造と設計の合意事項であるべきと思う。各部品の寸法は十分に管理され、その分布が平均値を中心とした正規分布となっていると仮定する。 この時のバラツキの程度を示すのが標準偏差σ、標準偏差の2乗が分散である。 平均値±σの範囲内に全体の6%、平均値±2σの範囲内に全体の954%、平均値±3σの範囲内に全体の997%が入る。 一般的に寸法は±3σの中に入るように管理されていることが多く、その場合の公差とは 信頼限界考え 信頼限界の計算 信頼区間の計算 計算(一変量) 二変量の較差(変数) 二変量標準偏差の計算式 二変量正規分布の確率の確認 二変量正規分布と確率 平均二乗誤差の式 平均二乗誤差と標準偏差の関係式 平均二乗誤差 平均二乗誤差と
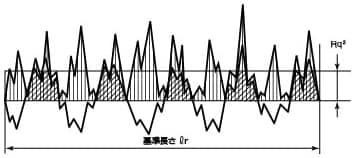
公差の 2448 ㎡から逆算すると,この場合の辺長は 1391 m から 1409 m の間である必要があります。面積で公差範囲内であるためには,位置誤差,辺長誤差がすべて平均二乗誤差の範囲にあってもその公差範囲に入ることは難しいようです。 現実的な問題算術平均粗さ: 基準長さにおける縦標値 𝑍(𝑥)の絶対値 の平均。 𝑹𝒒二乗平均平方根粗さ: 基準長さにおける縦標値 𝑍(𝑥)の二乗平 均平方根、粗さ曲線の標準偏差に相当する。 𝑍(𝑥) 𝑅 = 1 න 0 𝑙𝑟 𝑍(𝑥)𝑑𝑥 𝑅 = 1 න 0 𝑙𝑟 𝑍2𝑥𝑑𝑥過去の記事で「 公差の二乗和平方根をエクセルで計算してみた 」という公差計算について書きましたが、今回はその続きのお話です。 実際に部品が出来た時の測定結果について「バラツキ」を含めて考えるということについてです。 さてここで 「バラツキ! ? 何それ美味しいの? 」 「平均と何が違うの」 ってなる方に向けて詳しく説明をしていこうと思い
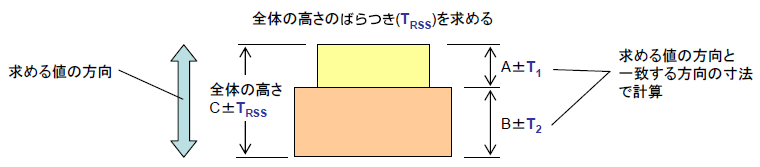
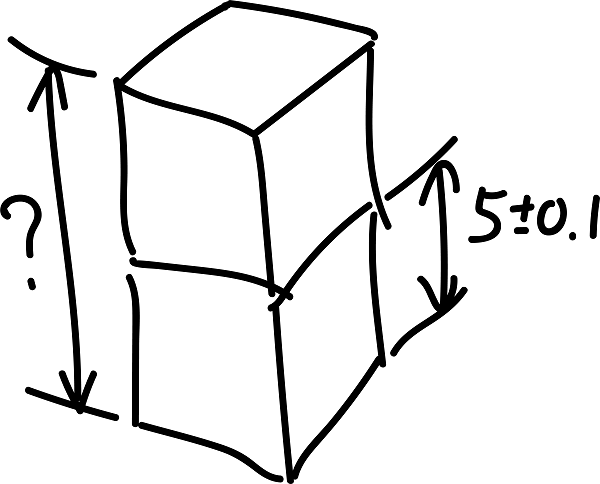
公差は約3倍平均二乗誤差に設定されています、平均二乗誤差と標準偏差の 関係は公差=424倍標準偏差になります、424σの確率は9999%である(甲2は 404σで9997%)です。 このことから不良率は001%以下を想定して別表第5の公差と平均二乗誤差が平均二乗誤差 公 差 地積測定の公差(㎡) 2㎝ 6㎝ 7㎝ ㎝ ( ( 15㎝ 45㎝ 25㎝ 75㎝ ( ( 150㎝ 100㎝ 300㎝ ( ( 工作の精度は一見甘すぎるように見えるが、永久標識であっても地下工作物の施工や地盤使用上の注意点 統計計算(二乗和平方根)での公差解析における注意点 ばらつきが正規分布で、公差域の中心に分布の平均値が来ることが前提。 計算に含める公差値の工程能力指数を合わせる。 計算に含める公差値の工程能力指数を揃える。 (例:すべてCp=1(3σ)とする) →求めた値の公差値も同じ工程能力指数値で算出される。 (T RSS もCp=1(3σ)での値



工程能力と公差解析 理論編と実践編



二乗和平方根とモンテカルロ法を比べてみた
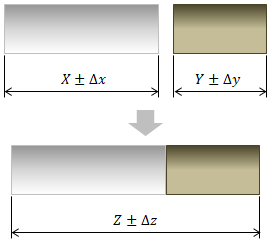
2乗平均⇒±mmが、今一つ??ですが、簡単に考えますと、 先ず、mm/025mm ≒ にて、平均の割合を出します。 そして、mm ÷公差の上下限値を積み上げて組立品質を求める 二乗和平方根 「分散の加法性」を使用し、発生する確率の低い最悪値同士の組合せは考慮から外して組立品質を求める方法。 公差を二乗して積み上げ、平方根で返した値を組立品質の予測値とする。公差の計算 精度区分 距離の公差点間距離(m) (×4√F)√F㎡ 面積F ㎡ 面積の公差0㎡ 筆界点の位置誤差(平均二乗誤差)2cm 筆界点の位置誤差(公差)6cm 株式会社 北辰測量設計



二乗平均平方根などの統計量について



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度
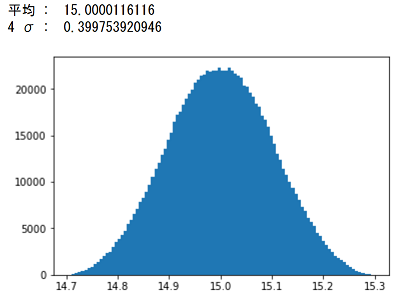
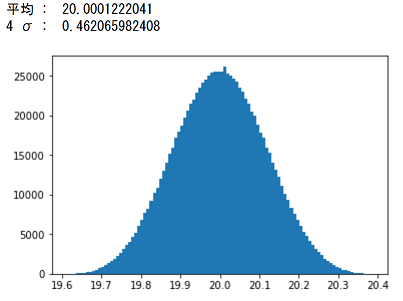
5(枚)≒ ±mm/枚となります。 次に、標準正規分布、板厚 5mm±005mmの公差005mmを35σと見なし公差計算(数値法)の概要 国土調査法施行令別表第四の公差計算(数値法)をします。 不動産登記規則第10条4 地図を作成するための一筆地測量及び地積測定における誤差の限度は、次によるものとする。 一 市街地地域については、国土調査法施行令二乗和平方根では元の寸法の分布は正規分布であるということが前提になります。 そこで、正規分布の乱数のマトリックスを2つ作って各要素を足してみます。 コードはこんな感じ。 Jupyter NotebookでPythonを使います。 もとの寸法はどちらも4σ(Cpk=133)の工程能力があるとします。 サンプル数は1,000,000個にしました。 計算結果はこうなります。 4σでの公差が




寸法公差について ご教示願います ワークを2本の位置決めピンと1枚のs Okwave



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度
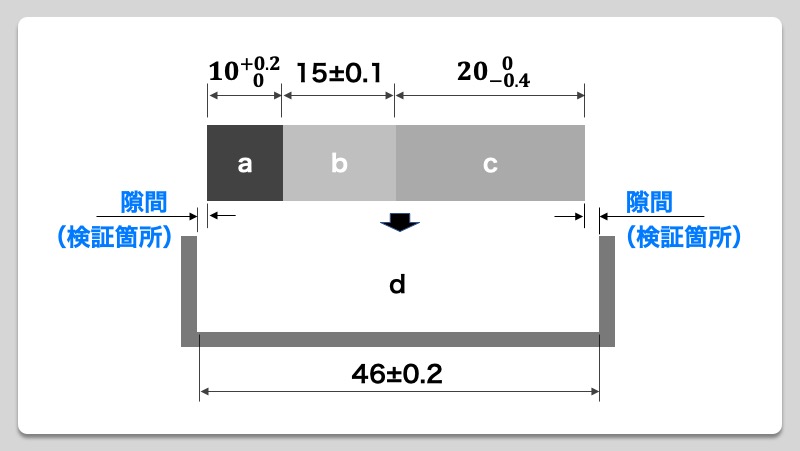
それに対して平均二乗誤差(Root Mean Square Error)とは求める値との差を評価する指標です。データを評価するとき標準偏差と言っ たり,平均二乗誤差と言ったり,中には平均二乗誤差(標準偏差)という者います,こうなると理RMSE (二乗平均平方根誤差)とは RMSEとは以下の数式で表される誤差のことで、予測と値がどの程度離れているのかを評価する関数です。 が機械学習モデルの予測した値で、が実際の正解データとなります。 この数式がどういう意味を持つのかを説明すると軸の軸受け当て面c~ボス当て面d 148 公差±05(中級加工公差) 累積誤差=√05^12^5^2=072 固定側 軸受台端面a~カバー側端面e 寸法235 公差±05(中級加工公差) カバー端面~羽根車ボス相対面g 24公差±02(中級加工公差) 累積誤差=√05^2^2=054



テクニカルレポート Busicom Post



1
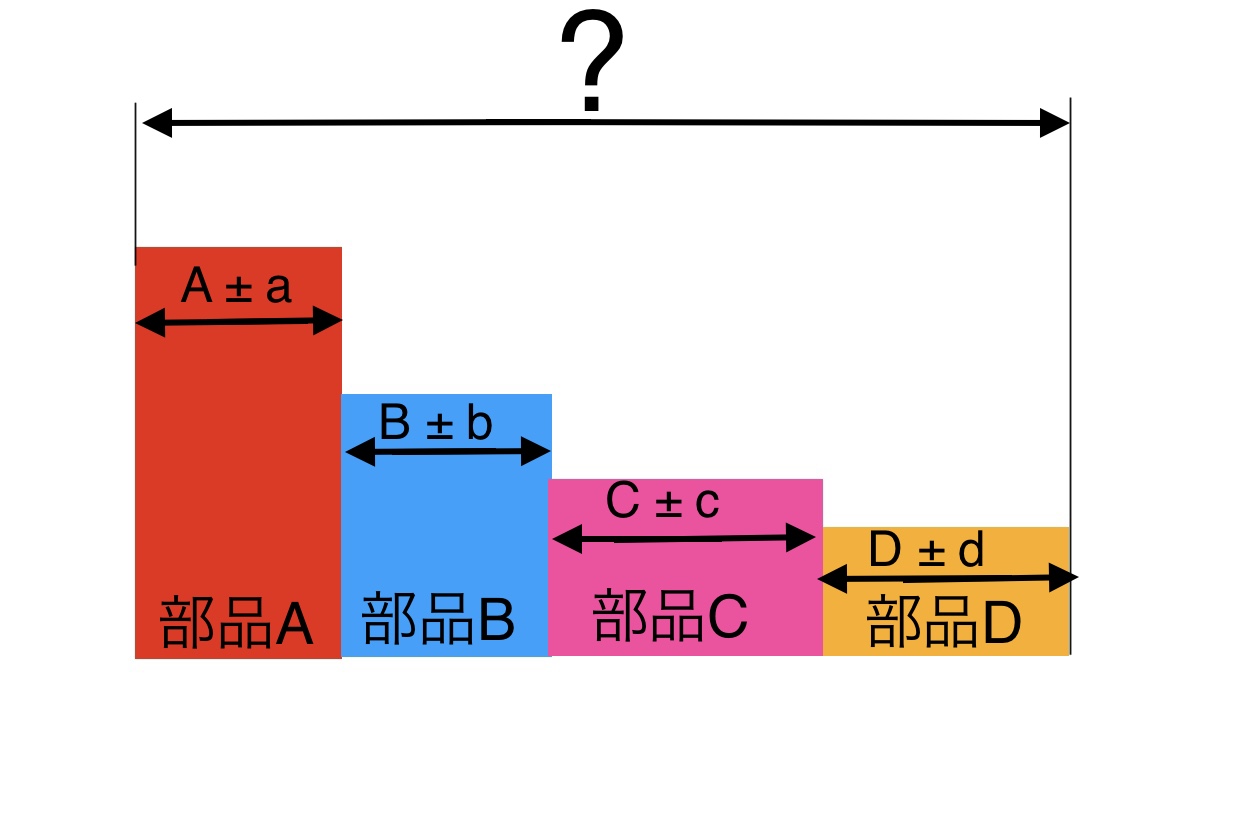
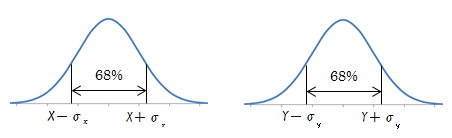
集積公差の正しいのはどちらですか??また、集積公差を外れる確率はなぜ3σなのですか?各部品寸法 A±a B±b C±cとあるとします。ABCは正規分布です。集積公差 = ±√(a^2b^2c^2)であるのか、集積公差 = ±√( (A部品のσ)^2 (B部品公差計算を行う際、計算結果の値が正規分布の "3σ:997%" の範囲内となる考えを元に、各公差を2乗和平方根を用いた累積計算を行います。 この2乗和平方根による公差計算ですが、過去に私が統計学の正規分布を少しかじり始めた頃、"3σ:997%" ではなく "標準偏差σ:6%" の部分を計算しているように思え、疑心暗鬼に陥ったことが度々ありました。 少し




05 機械設計 公差の二乗和平方根をエクセルで計算してみた 基礎知識 好きな事で生きていく



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes



Http 012 O Oo7 Jp My webs03 K Hyoujyunhensa Kousa Pdf



二乗平均



技術計算製作所 公差の考え方 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Mech Engineer General Tol




テクニカルレポート Busicom Post




公差計算と幾何公差1 ライブラリ Opeo 折川技術士事務所



二乗平均平方根などの統計量について



累積公差の計算 二乗和平方根 製品設計知識




分散の加法性 ライブラリ Opeo 折川技術士事務所




統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から
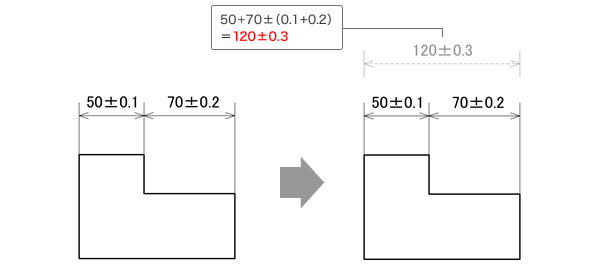



寸法公差の妥当性を検証する 世界で戦えるglobalエンジニアになるための製図技術 4th Step 第5回 お客様マイページ 大塚商会
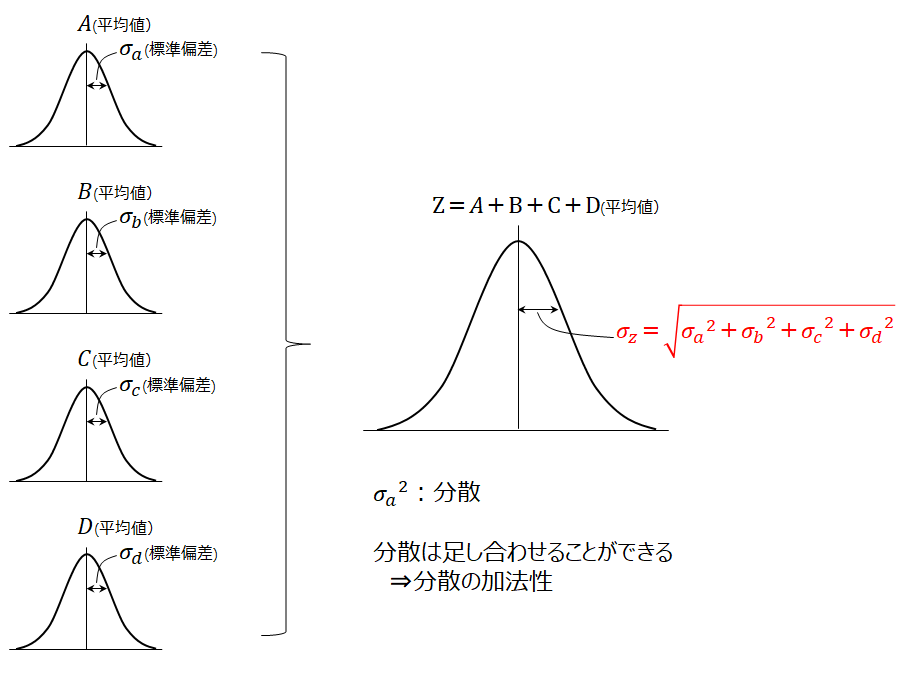



累積公差の計算 二乗和平方根 製品設計知識
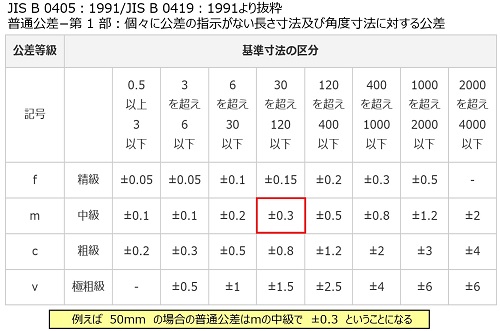



テクニカルレポート Busicom Post



5 累積公差とは 株式会社 ケープヒル コンテムズ
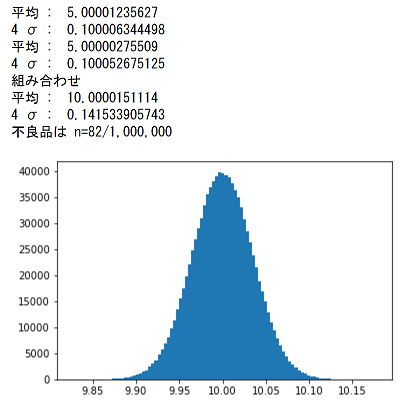



二乗和平方根とモンテカルロ法を比べてみた
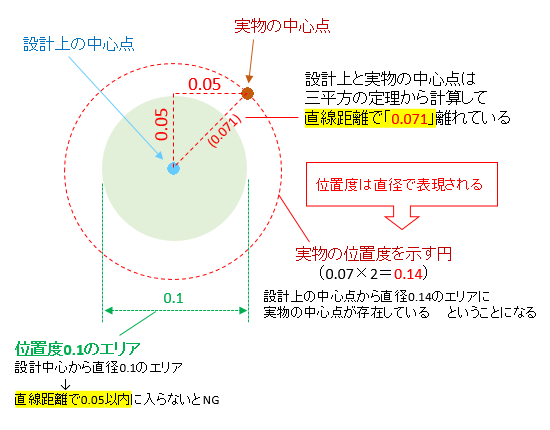



位置度の計算方法を調べてみた 試作メーカー渡辺製作所 単品加工ok



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度




統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から




誤差と相対誤差 ライブラリ Opeo 折川技術士事務所




第2回 どうやって特性の公差を合成するか 2ページ目 日経クロステック Xtech



初心者でもできる公差計算 実践編 緊度計算 累積公差 二乗平均公差




二乗平均平方根 Wikipedia




ピックアップ プリント基板の窓口 プリント基板設計 製造 実装の最適な発注先が見つかる



平均二乗誤差




05 機械設計 公差の二乗和平方根をエクセルで計算してみた 基礎知識 好きな事で生きていく




公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット




公差累積解析のタイプ



Ky Yoso 1si
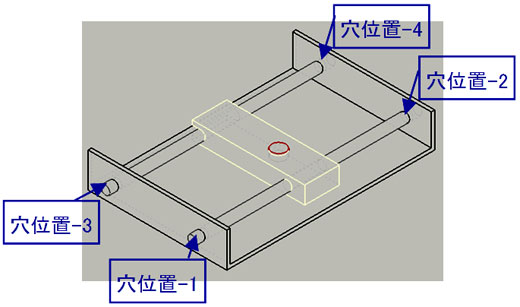



公差解析の基本おさらいタイム始まるよ 公差解析 基本中の基本 8 3 3 ページ Monoist
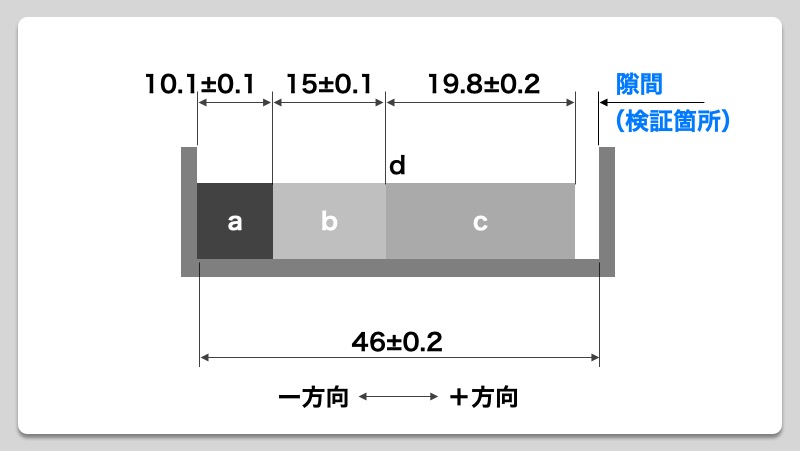



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
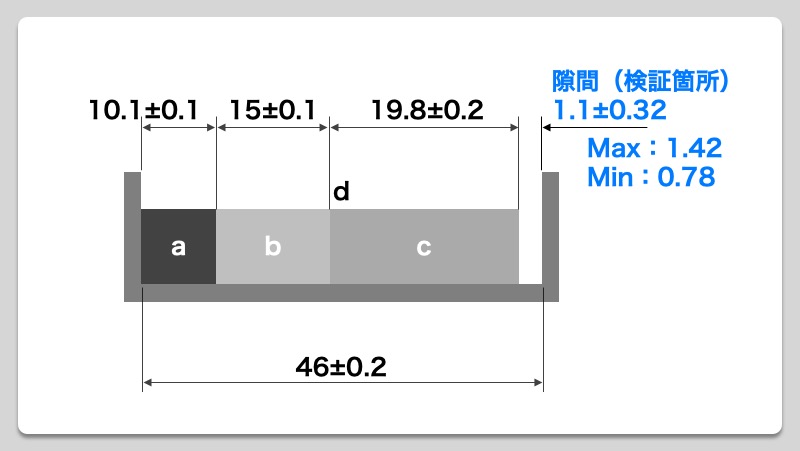



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes




製品設計のいろは 公差計算 2乗和平方根と正規分布3sの関係性 Show Notes



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度
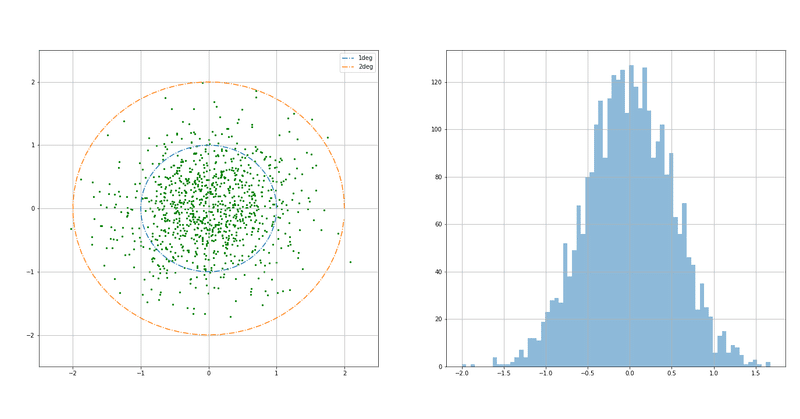



機械系エンジニアのためのpythonを用いた公差解析 かす Note



テクニカルレポート Busicom Post




累積公差の計算 二乗和平方根 製品設計知識




統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から



3




公差に対する思い込み 日経クロステック Xtech
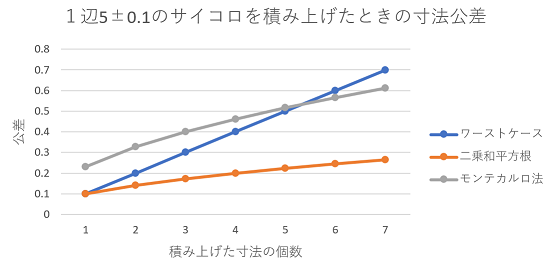



二乗和平方根とモンテカルロ法を比べてみた
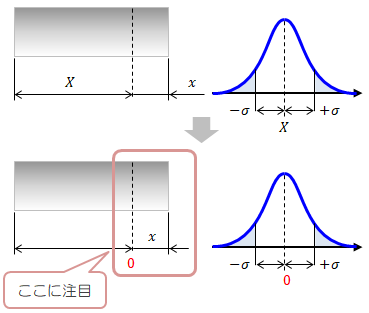



技術計算製作所 公差の考え方 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Mech Engineer General Tol




機械系エンジニアのためのpythonを用いた公差解析 かす Note



5 累積公差とは 株式会社 ケープヒル コンテムズ



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes



初心者でもできる公差計算 実践編 緊度計算 累積公差 二乗平均公差




二乗平均平方根 Wikipedia



二乗和平方根とモンテカルロ法を比べてみた
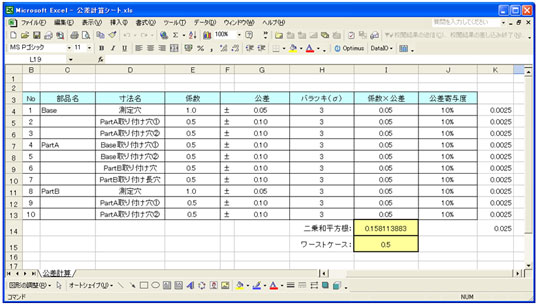



公差計算excelシートにシビレちゃいなyo 公差解析 基本中の基本 7 4 4 ページ Monoist




製品設計のいろは 公差計算 2乗和平方根と正規分布3sの関係性 Show Notes



1




概要 公差解析 Inventor Autodesk Knowledge Network




製品設計のいろは 公差計算 2乗和平方根と正規分布3sの関係性 Show Notes



Http 012 O Oo7 Jp My webs03 K Hyoujyunhensa Kousa Pdf



積み上げ公差の計算をするとき 二乗平均を使う 使える のはなぜです Yahoo 知恵袋
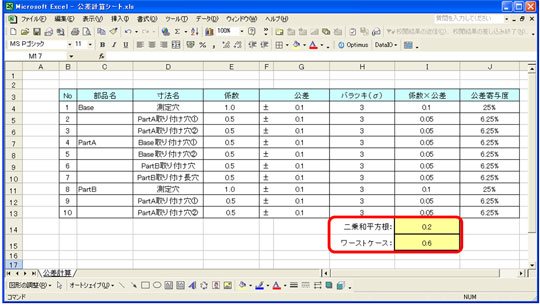



公差計算excelシートにシビレちゃいなyo 公差解析 基本中の基本 7 4 4 ページ Monoist



05 機械設計 公差の二乗和平方根をエクセルで計算してみた 基礎知識 好きな事で生きていく




公差計算と幾何公差1 ライブラリ Opeo 折川技術士事務所



設計などでよく使用されている平均二乗誤差の計算方法を教えてください Yahoo 知恵袋



本来の境界位置との許容誤差 交差



製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes



初心者でもわかる複数部品の公差の積み重ね 累積公差 二乗平均公差 絶対緊度




公差分析編 ライブラリ Opeo 折川技術士事務所




教科書にはない機構設計ノウハウ 公差編 合同会社エスキージャパン
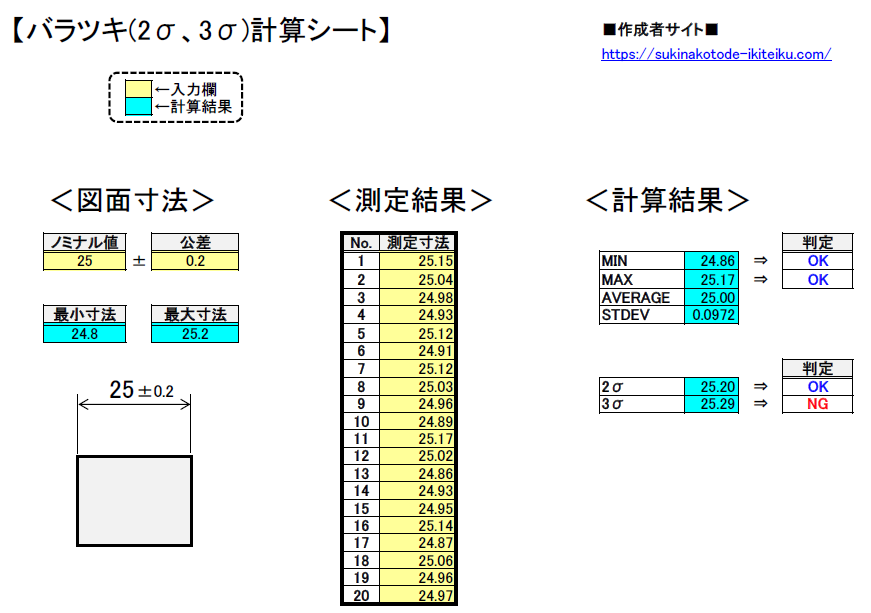



13 機械設計 標準偏差のばらつき 3s の公差計算エクセルシート 好きな事で生きていく




製品設計のいろは 2乗和平方根で公差計算を行うための3つの手順 Show Notes
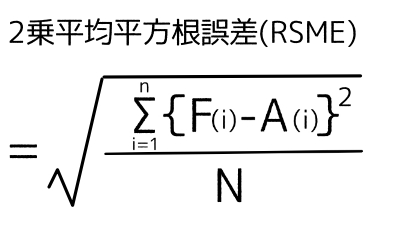



二乗平均



平均二乗誤差
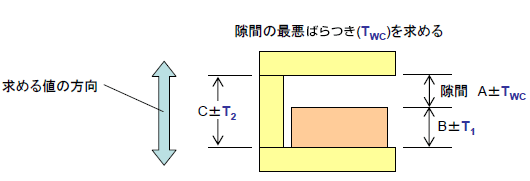



公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット
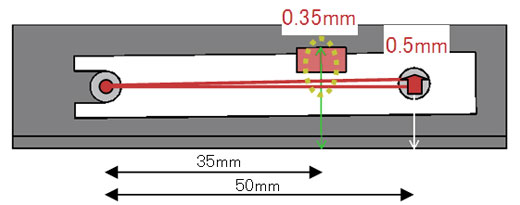



公差解析の基本おさらいタイム始まるよ 公差解析 基本中の基本 8 3 3 ページ Monoist




公差計算 数値法 プログラム Fx 5800p測量計算 あさかぜネット
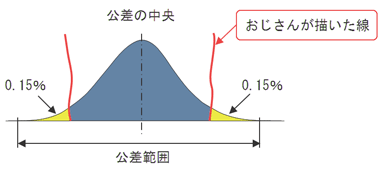



ワーストケースと二乗和平方根って 何 公差解析 基本中の基本 2 3 4 ページ Monoist
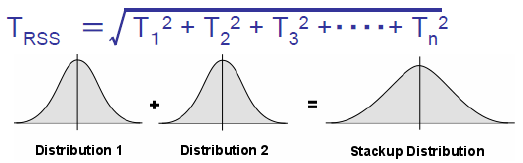



公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット



1




公差計算の基本手法 ライブラリ Opeo 折川技術士事務所




標準偏差って何 例題でわかりやすく順を追って解説 正規分布も噛み砕いてみました 機械設計者の皆様 教わらなかったことは常識だそうです



累積公差の計算 二乗和平方根 製品設計知識




第3回 公差設計の実践 日経クロステック Xtech




教科書にはない機構設計ノウハウ 公差編 合同会社エスキージャパン



公差設計




最小二乗平均って何 Youtube




教科書にはない機構設計ノウハウ 公差編 合同会社エスキージャパン



技術計算製作所 公差の考え方 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Mech Engineer General Tol



公差解析手法 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット



二乗和平方根とモンテカルロ法を比べてみた



二乗平均平方根などの統計量について
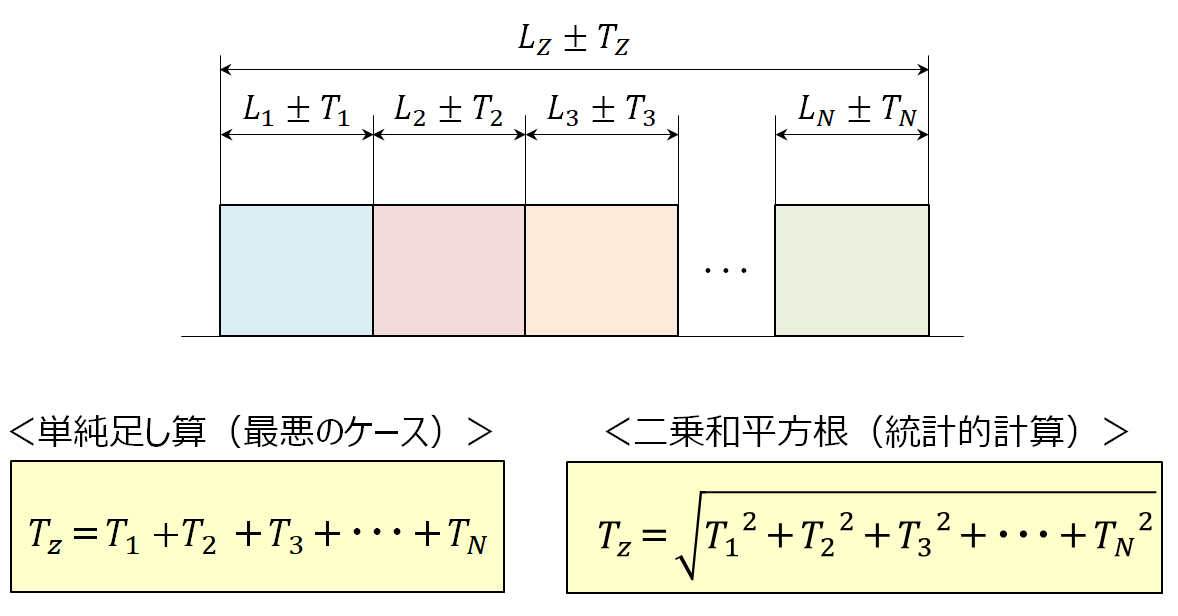



累積公差の計算 二乗和平方根 製品設計知識



本来の境界位置との許容誤差 交差



二乗平均平方根などの統計量について
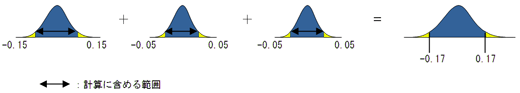



ワーストケースと二乗和平方根って 何 公差解析 基本中の基本 2 4 4 ページ Monoist
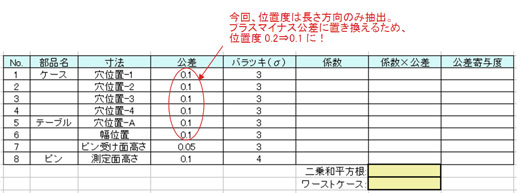



公差解析の基本おさらいタイム始まるよ 公差解析 基本中の基本 8 3 3 ページ Monoist
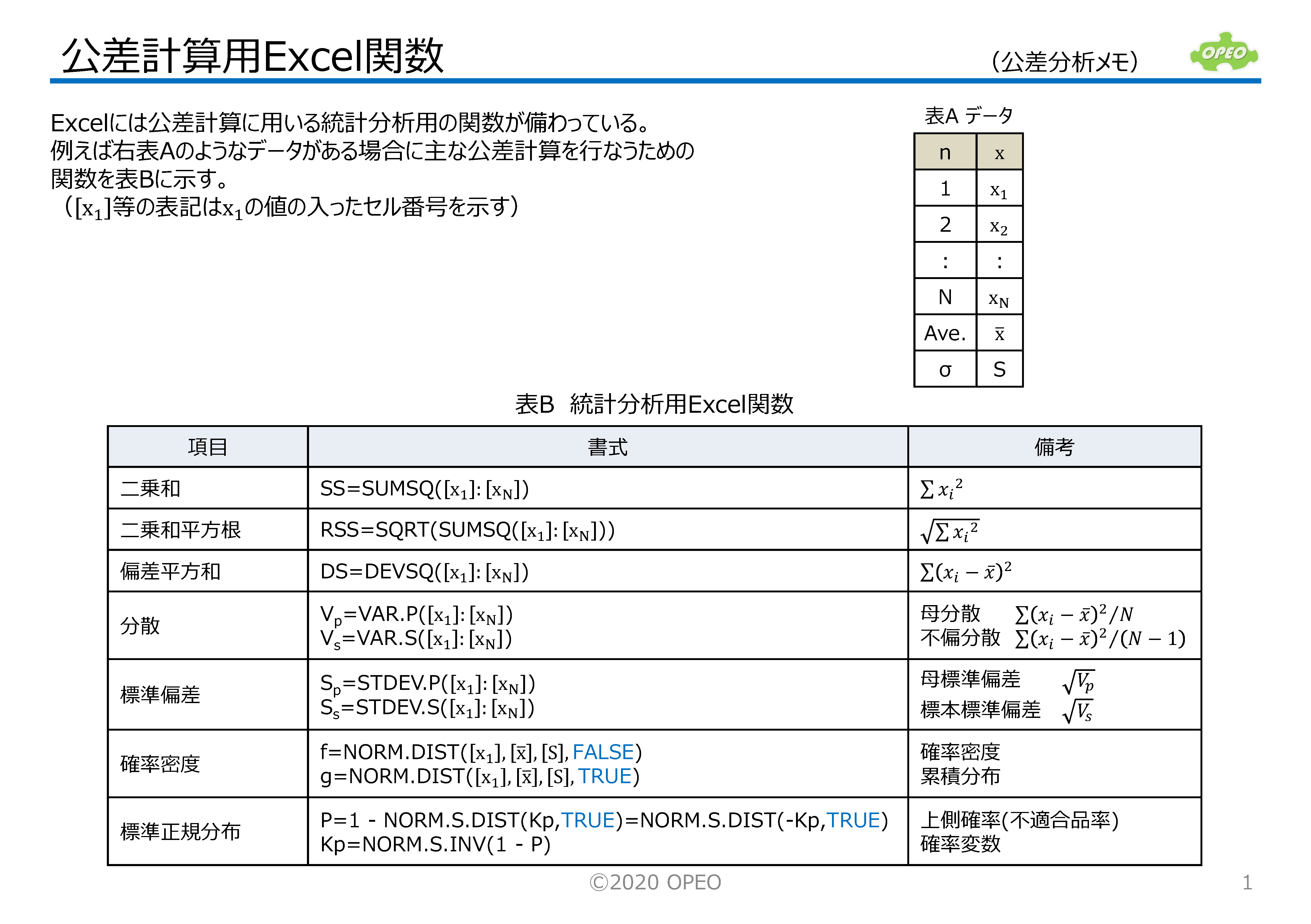



公差計算用excel関数 ライブラリ Opeo 折川技術士事務所
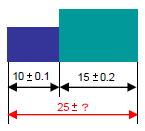



従来の公差計算と問題点 公差解析入門 公差解析の効率化 幾何公差化の実現に Cetol 6s サイバネット
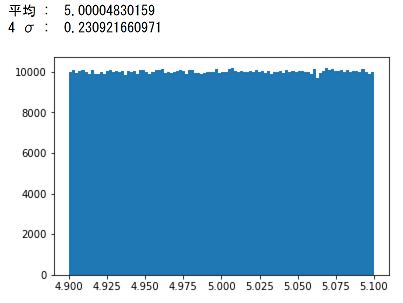



二乗和平方根とモンテカルロ法を比べてみた




公差累積解析のタイプ



統計的に正しいけど 累積公差計算 二乗和平方根 の基本と限界 wicの中から



コメント
コメントを投稿